Look at these people. They look gorgeous, don’t they? Well, too bad they do not exist. These images are completely synthetic. How is it possible, by the way? Well, thanks to a Deep Learning architecture called Generative Adversarial Networks (GANs) [1]. Long story short, these architectures are able to capture the probability distribution of a training set (of images, in this case) and to replicate for creating a new sample with the same probability distribution (therefore realistic) but not belonging to the training set. In a nutshell this architecture is made up of two building blocks. A Generator (G), an artificial neural network that takes as input a noisy vector and tries to fool a Discriminator (D, another neural network) by generating more and more realistic images. D has the task of distinguishing between synthetic images (generated by G) and realistic images (the one of the actual training set) by highly penalizing G if it is easily able to label the synthetic images as “fake” and by less penalizing G it is hard to distinguish synthetic and real images. You can find a schema of a classic GAN in Figure 1.

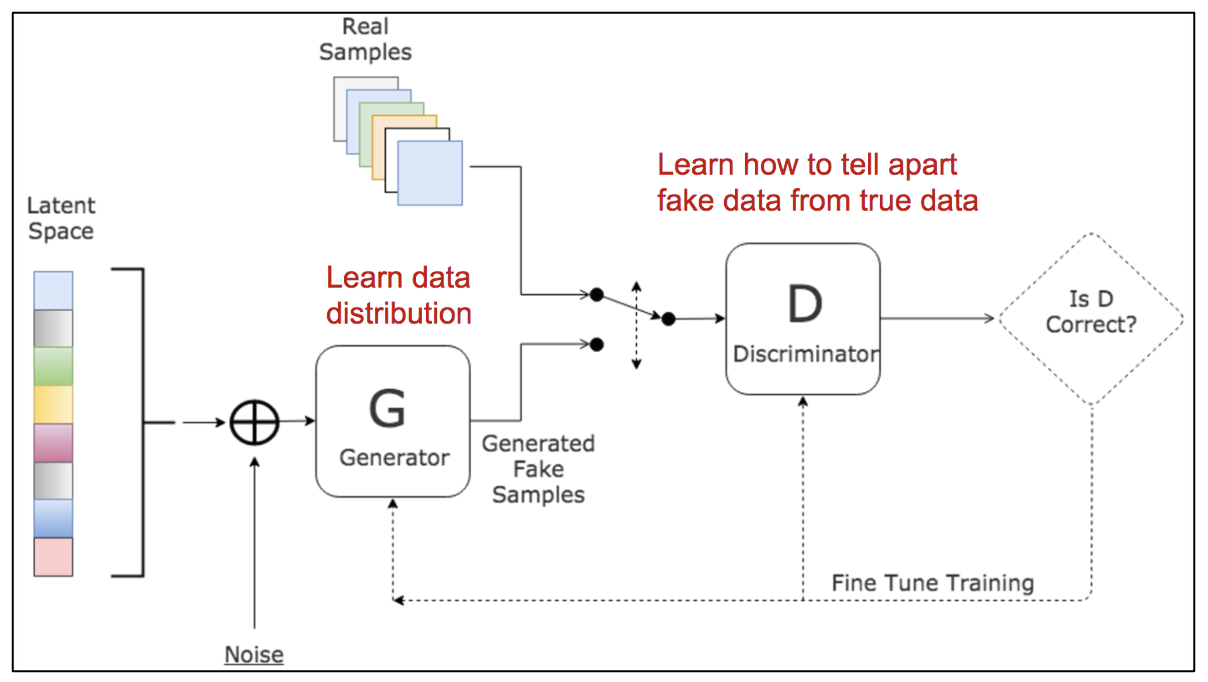
Figure 1: Classical GAN architecture.

What if I tell you that we can use this architecture to study and generate daily mobility flows in a city? Well, let’s fix some definitions first.

First of all a tessellation is a partition of a city in (regular and squared in our case) zones called tiles. A Mobility Network (MN) is a weighted directed network in which nodes are tiles and edges represent the number of people moving between tiles. We represent a Mobility Network as a Weighted Adjacency Matrix (See Figure 2).

But what have GANs to deal with Mobility Networks?

Well, if you think about it a matrix can be seen as a mono-channel image (Figure 2), so here it’s our intuition:

            If we are able to generate synthetic images of different people, we can be able to generate synthetic matrices representing daily Mobility Networks of a city.

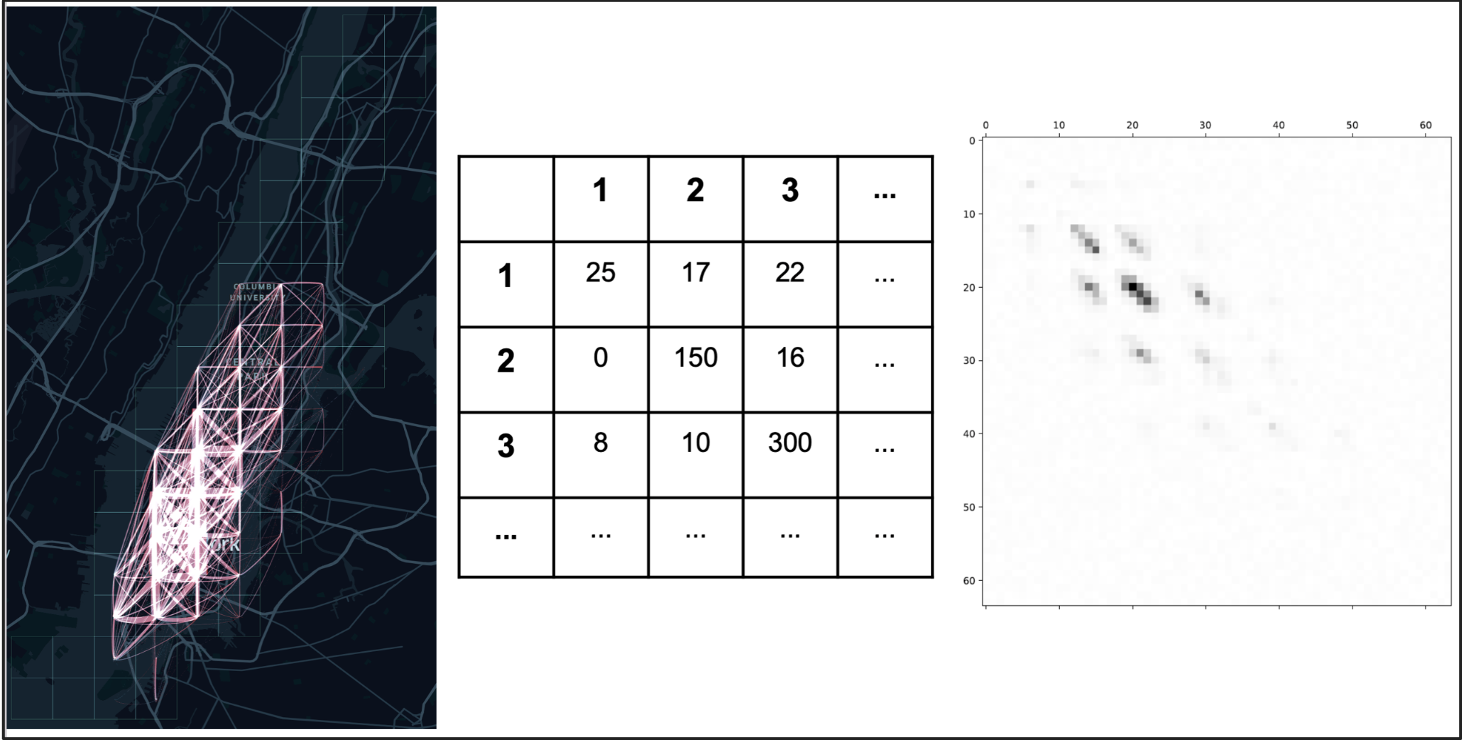
Figure 2: From left to right: Visual, Matrix and b/w image representation of a daily MN

We therefore introduce: MoGAN (Mobility Generative Adversarial Network) [3]. MoGAN is based on Deep Convolutional GAN (DCGAN) [2] a particular type of GAN in which both G and D are Convolutional Neural Networks (CNNs): G performs an upsampling convolution (i.e. it takes a noisy vector as input and transforms it into a synthetic matrix), while D performs the classical convolutional classification. In our case, MoGAN will operate over a training set of daily Mobility Networks and at the end of the training process MoGAN’s Generator will be able to generate as many fake Mobility Networks as desired (see Figure 3). DCGAN specifics require images (matrices) to be of dimension 64x64, this is why we split the city into 64 equally spaced squared tiles, so as to have the adjacency matrices of the mobility networks of dimension 64x64.

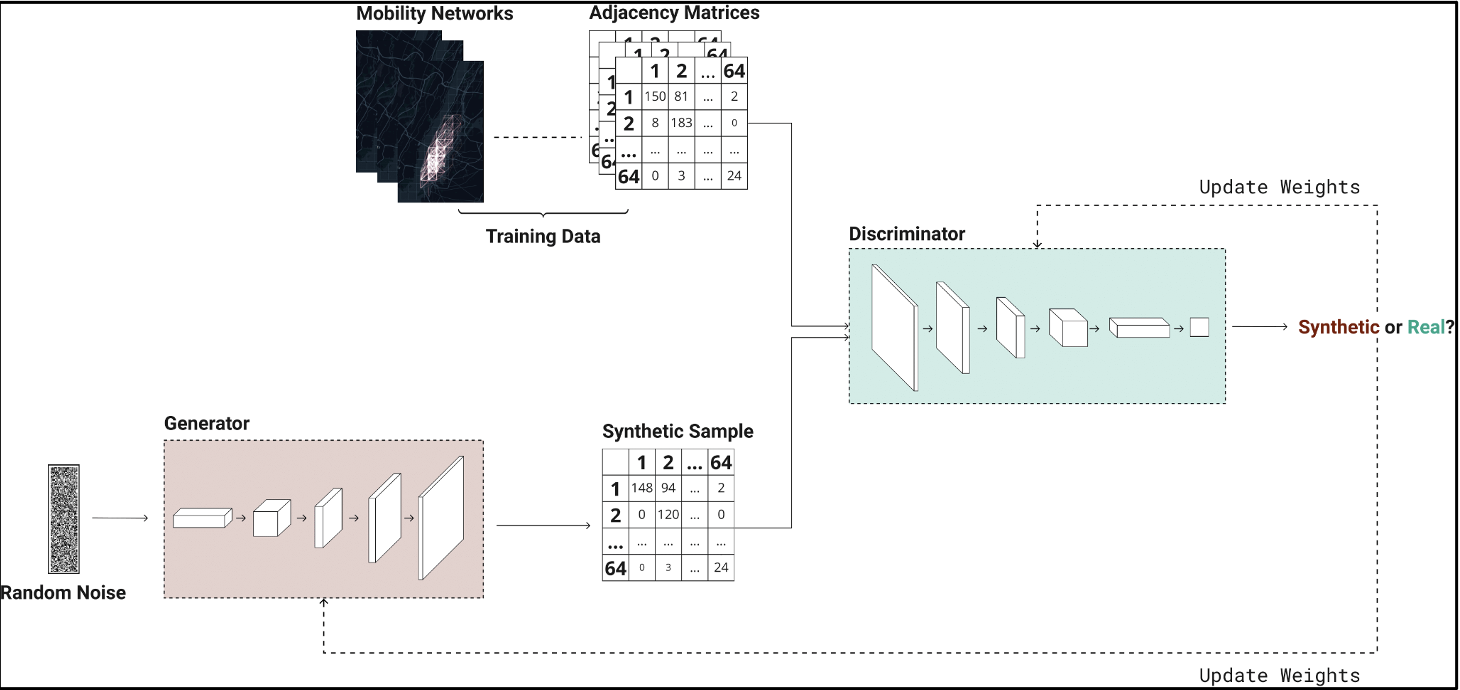
Figure 3: MoGAN architecture.

We train MoGAN over 4 different datasets. MoGAN is able to generate synthetic networks of two different means of transport (bike and taxis) and of two different cities (New York City (NYC) and Chicago (CHI)). For all of these 4 datasets, we transform the tabular data in input (each row containing information of the starting and ending zone of the bike or taxi ride) into a 64x64 adjacency matrix representation.

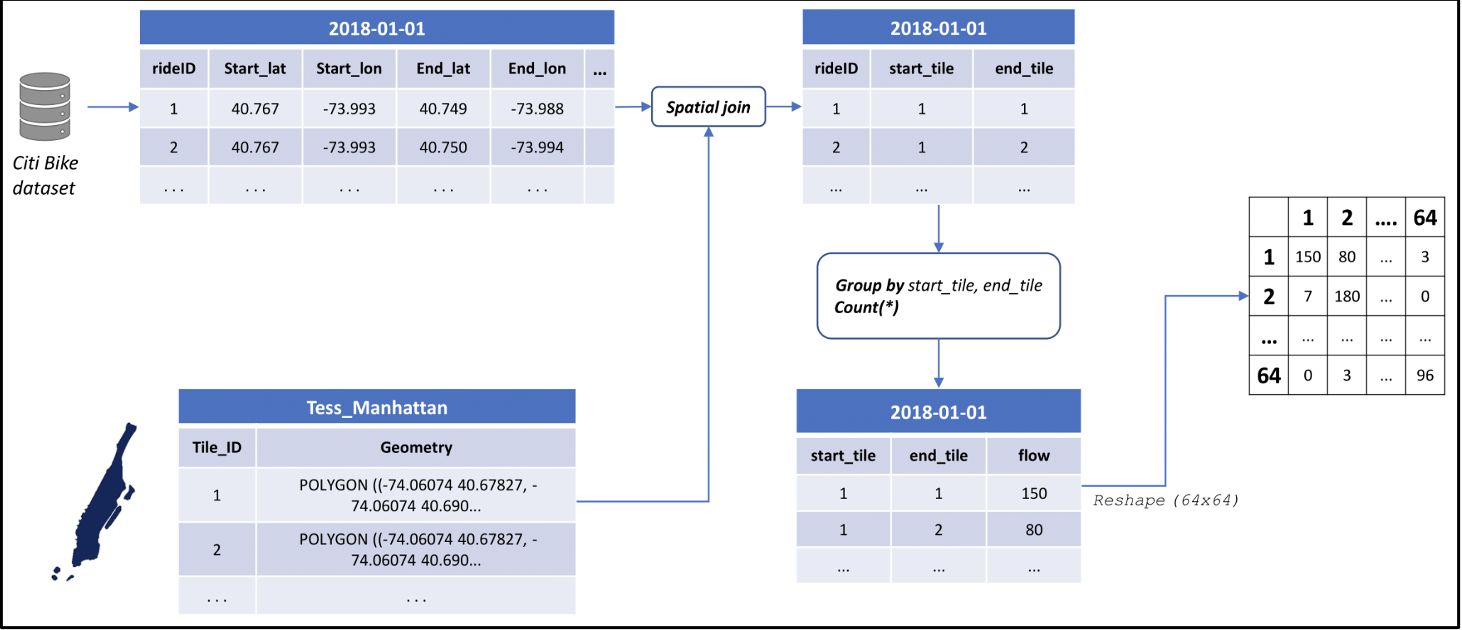
Figure 4: Data Extraction and Transforming phase for NYC’ bike dataset.

We do that by performing a spatial join operation with the tessellation of the city, grouping and counting the rides starting and ending in each tile and transforming the dataset into a list of 64x64 daily arrays. A visual representation of the transformation into Mobility Networks for the NYC’ bike dataset is given in Figure 4.

Ok, so now MoGAN is able to generate tons of realistic Mobility Networks. How do we evaluate its actual generative ability? In fact, evaluating if a face is realistic it’s quite easy: we can look at the picture and decide if it is realistic or not! On the other hand, deciding if a network is similar to another is not so easy. In order to do so we compare our model with two classical mobility models for flow generation: Gravity[4] and Radiation[5] model. Gravity model postulate that the flows between two locations is inversely proportional to the distance between them, while the Radiation model considers the number of opportunities in each place, along with the distance, when generating flows.

For comparing our model with these baseline models, we create three sets:

●      Test Set: A set of networks excluded from the training phase

●      Synthetic Set: A set of fake networks generated by MoGAN

●      Mixed Set: A set of networks coming half from the Training Set and half from the Synthetic Set

After that, we calculate the distribution of several similarity measures (CPC, RMSE, JS divergence of the Weight distribution and several more). We would like the distribution over the three sets to be as much overlapping as possible. As you can see in Figure 5 that reports the results of the CPC analysis, the three distributions of our models are way more overlapping than the distributions of the other two models, for all of the 4 datasets!

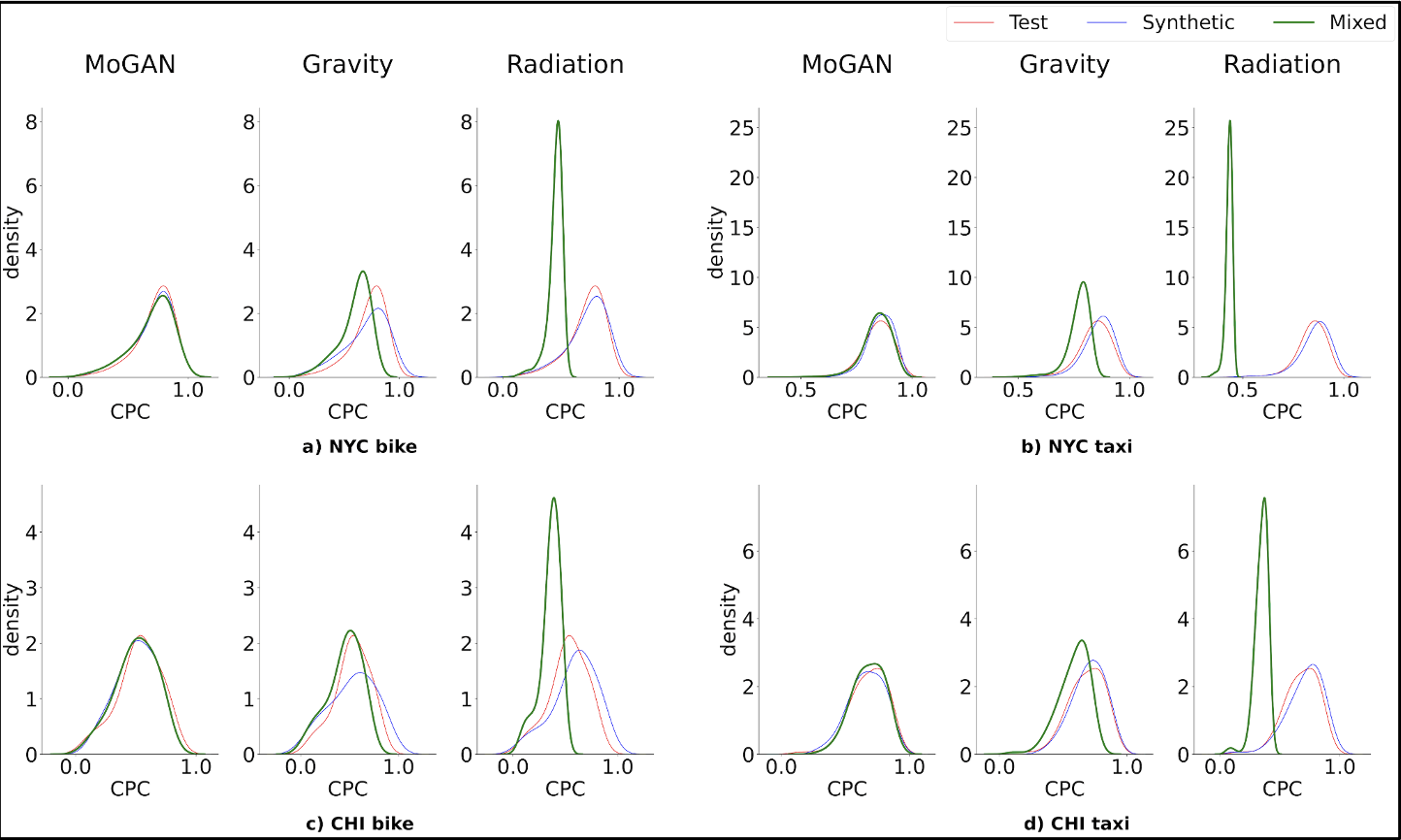
Figure 5: Distribution over the Test, Synthetic and Mixed set of the CPC scores of MoGAN over the three datasets

Nice work, but… What’s the point of generating synthetic Mobility Networks?

Well, several uses actually. Retrieving quality mobility data is hard, due the well-known privacy issue when dealing with such sensitive data. Therefore a tool such as MoGAN allows a useful way for performing high-level data-augmentation operations. Furthermore, our model can be used as a useful what-if simulation tool.

P.S. our model and analysis is completely reproducible:

Visit https://github.com/jonpappalord/GAN-flow

Author: Giovanni Mauro | PhD UNIPI

BIBLIOGRAPHY

[1] Goodfellow, Ian, et al. "Generative adversarial nets." Advances in neural information processing systems 27 (2014).

[2] Radford, Alec, Luke Metz, and Soumith Chintala. "Unsupervised representation learning with deep convolutional generative adversarial networks." arXiv preprint arXiv:1511.06434 (2015).

[3] Mauro, Giovanni, et al. "Generating Synthetic Mobility Networks with Generative Adversarial Networks." arXiv preprint arXiv:2202.11028 (2022).

[4] Barbosa, Hugo, et al. "Human mobility: Models and applications." Physics Reports 734 (2018): 1-74.

[5] Simini, Filippo, et al. "A universal model for mobility and migration patterns." Nature 484.7392 (2012): 96-100.