Learning latent low-dimensional vectors of network’s nodes is the central aim of GRL [1], and nowadays node embeddings are crucial in order to solve machine learning tasks on graphs. Usually they are computed with self-supervised training, using edge reconstruction as a pretext task [2], with the result of encoding node proximities into distances of a metric space. According to this strategy, common to many algorithms such as DeepWalk and Node2Vec [2], inner products between node embedding pairs are proportional to the likelihood of observing the corresponding edge on the training graph.

Node representations are understandable only in terms of their pairwise geometric relationships, and interpretations of individual embedding dimensions are typically hard to provide [3]. Here we define the interpretability of node embedding vectors assigning a human-understandable meaning to representation dimensions. In particular, we aim to associate different dimensions with different graph partitions [4]. In fact, densely connected subgraphs describe groups of nodes highly related to each other, like groups of similar words appear together when talking about a given topic [5].

We designed an algorithm that, given a set of node embeddings previously trained, returns a new set of post-processed node representations with a human-interpretable meaning. This is possible by means of autoencoder neural networks [6], which efficiently map input vectors into a new embedding space where we enforce interpretability constraints. In particular, we require orthogonality among clusters of edges reconstructed with different dimensions, in addition to calibrating new representations to ensure that all dimensions reconstruct a non-null subset of links.

In Figure 1 we see how the algorithm works on a toy graph with 4 densely connected communities arranged in a ring, i.e. a ring-of-cliques graph. We show, for any edge, variations of inner product scores (edge importance) occurring when removing the corresponding feature from 4-dimensional node vectors. As compared to input DeepWalk vectors, our technique leads to more interpretable edge reconstruction patterns on the output.

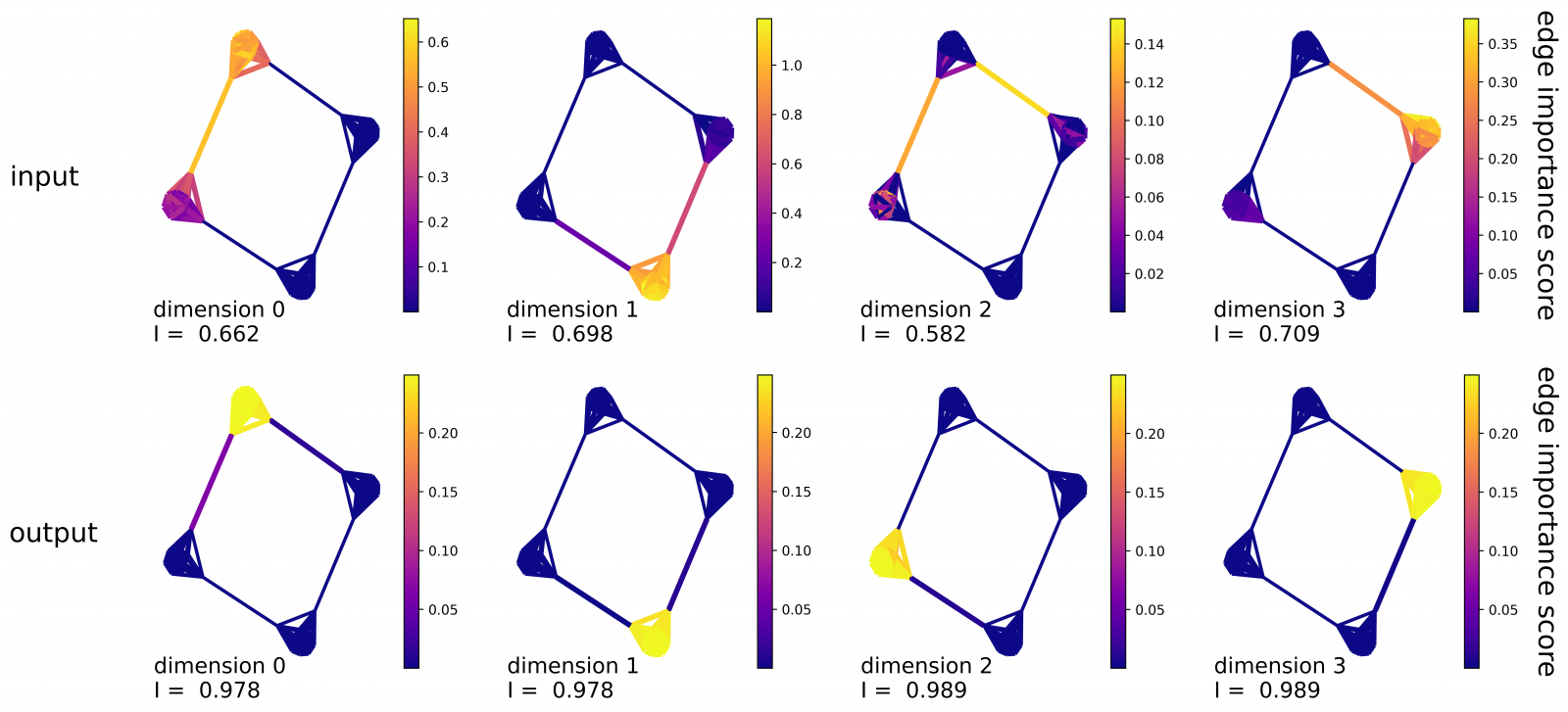
Figure 1: Edge importance scores computed with 4-dimensional embeddings on a ring-of-cliques graph: (Top) input DeepWalk; (Bottom) output for our model.

In fact, links from the same community receive high contributions by one unique dimension. Interpretability of dimensions is assessed by a score which quantifies how well the reconstructed edges match with a given partition.

Figure 2: Accuracy and Fidelity gains between input DeepWalk and our output: (Left) visualization of Cora graph, image from https://arxiv.org/abs/1611.08402; (Top Right) ratios of average interpretability dimensions scores; (Bottom Right) ratios of average link prediction scores.

In Figure 2 are shown the effects of our algorithm on the Cora citation network [7]. Nodes belonging to the same research topic are more likely to connect with each other, forming densely connected clusters. On the right (Top) we evaluate the accuracy [8] of interpretations, i.e. the level of alignment between representation dimensions and ground-truth topics. On the right (Bottom) we evaluate the fidelity [8] of interpretations, i.e. the link prediction agreement between the interpretable model and the input model. We observe, for our technique, increments in scores for interpretability (up to 80%) and link prediction (up to 10%), with respect to input DeepWalk vectors.

We have similar findings on multiple datasets, opening the path to new research investigations on the interpretability of unsupervised graph representation learning.

References: