Network Medicine: Disease Genes Prioritization Problem
Exploratory: Network Medicine
Today, big data, genomics, and quantitative in silico methodologies integration, have the potential to push forward the frontiers of medicine in an unprecedented way [1, 2]. Clinicians, diagnosticians and therapists have long striven to determine single molecular traits that lead to diseases. What they had in mind was the idea that a single golden bullet drug might provide a cure. Unfortunately, individual diseases rarely share the same mutations. This reductionist approach largely ignores the essential complexity of human biology. Indeed, a large body of evidence that is now emerging from new genomic technologies, points out directly to the cause of disease as perturbations within the Interactome, i.e. the comprehensive network map of molecular components and their interactions.
One crucial Problem in Network Medicine we are investigating, consists of prioritizing candidate disease proteins, i.e. product of genes whose mutation gives rise to a cellular function and its disruption ends up in a specific disease phenotype. Disease proteins may provide targets for different kinds of disease therapy, but there are complications depending not only on the phenotype but also on different factors that are patient specific. These considerations directly point towards the possibility that, whenever a disease module sub-network is found, other disease-related parts are likely to be identified in their topological neighborhood [3].
The need for new disease genes (or disease proteins) as putative candidates for diagnosis, treatment or drug targeting, motivated the development of a number of algorithms for predicting disease genes and modules.
Disease-Gene prioritization. is the process of assigning likelihood of gene involvement in generating a Disease D. Network based approaches to gene prioritization aim to identify candidate genes using Disease information (i.e known disease proteins involved in phenotype) and Network Information such as Protein Protein interaction (PPI) network in which proteins are nodes and there exists a link between protein pairs if they physically interact.
Random Walks with Restart can be seen as performing multiple random walks over the PPI network, each starting from a seed node associated to a known disease gene, iteratively moving from one node to a random neighbour,thus simulating the diffusion of the disease phenotype across the interactome. More formally, the random walk with restart is defined as: p(t+1) = (1 − r)W p(t) + rq. (1). Here, W is the column-normalized adjacency matrix of the graph and p(t) is a vector, whose i-th entry p(t) is the probability of the random walk being i at node i at the end of the t-th step. r ∈ (0, 1) is the restart probability, i.e., the probability that the random walk is restarted from one of the (disease- associated) seed nodes in the next step.
Biological Random Walks. In [4], we present a new algorithm (Biological Random Walks) that weights the transition matrix W and the personalization vector q using biological and genomics information. Both annotation data and gene expression levels allow derivation of person- alization vectors that reflect some notion of similarity between a gene and a disease, i.e. its seed genes.
Biological Annotation. Given l sources of biological information and S the seed set: for every j = 1,...,l, we use Fj to denote the subset of annotations from the j-th source that are associated with genes in S, so that F = ∪lj=1Fj denotes the set of all annotations that are associated with genes in S. Likewise, for every gene i (not necessarily belonging to S), we denote by A(i) the set of its annotations, possibly extracted from multiple biological information sources. We next assign each gene i a weight θi as follows:
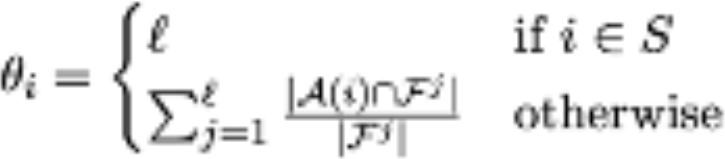
At this point components of a personalization vector q can be computed as follows:
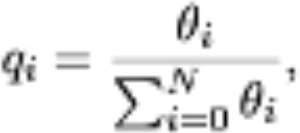
with N the number of genes we consider. Note that qi denotes the probability that, upon teleportation, the random walkers jump to gene i. Using gene expression data. Similar approaches can be used to derive a transition matrix for the random walk with restart. In this case, we consider a weighted transition matrix W, in which each entry Wij depends on the extent to which nodes genes i and j of the PPI share common annotations (i.e., they are involved in common biological processes) that are also significant for the disease:
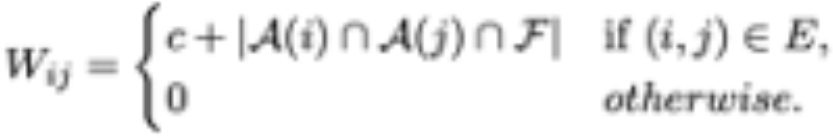
Here, c is a positive constant that accounts for usual sparsity of the available datasets, so that no biological information may be available for the end- points of a link in the PPI. In this case, the link receives a minimum weight c.
Gene expression. To identify Differentially Expressed (DE) genes, we used gene expression levels of case (Disease) and a control (Healthy) group. Integrating Biological Information and Gene Expression After the computation of the biological and the gene expression personalization vector respectively named q1 and q2, the framework compute the final q as convex combination of q1 and q2: q = αq1 + (1 − α)q2. Having gene expression profiles of a number of genes for several samples or experimental conditions, a gene co-expression network can be obtained by identifying gene pairs that show similar expression patterns across samples. One way to create this network is to use the Pearson’s Correlation coefficient that is a measure of the linear correlation between two variables. Computing an Aggregate Transition Matrix Assume we have computed transition matrices W1 and W2 using biological and gene expression information respectively. We proceed in a way that is similar to the approach used to derive an aggregate personalization vector. Indeed, we consider the convex combination of adjacency matrices W1 and W2 defined as W = βW1 + (1 − β)W2.
Validation. We first conducted an internal validation, performing a Monte Carlo cross- validation on ‘gold standard’ gene sets. We created multiple random splits of the OMIM associated genes, with each random split consisting of a subset of seed genes( 70% of the total) and a test set accounting for the remaining 30% of the genes. For each split, we prioritized genes using BRW with seeds genes to compute a ranking of the genes. Only the top 200 genes were con- sidered as potential candidates. We then used test genes to assess predictive accuracy of the algorithm in terms of Recall@K comparing BRW with well known heuristics such as DIAMOnD (Menche et al. 2015) and Random Walks with Restart (Koler et al. 2009). BRW outperforms both RwR and DIAMOnD with a Recall@K score of 0.425, while DIAMOnD and RwR got 0.22 and 0.24 respectively.
Furthermore, we validate candidate genes predicted by each algorithm con- sidering the topology of the predicted modules and the relation between prioritized genes and drugs related to Breast Cancer disease.
First, the density of BRW candidates is higher than the sub-graphs in- duced by RwR and DIAMOnD prioritized genes. Furthermore, seed genes are closer to each others in BRW sub-graph as shown in Figure 1 ii). Fi- nally, for each set prioritized by each heuristic, we compute the statistically significant drugs (corrected p-value < 10−5) of each the candidate set as shown in Figure iii). Gene set predicted by BRW is far more enriched in letrozole,ribavarin and tamoxifen that have been used to treat breast can- cer disease. It’sworth nothing that some drugs are enriched only by BRW like Paclitaxel, Bexatorene and Bexatorene that are currently in clinical trial phase.
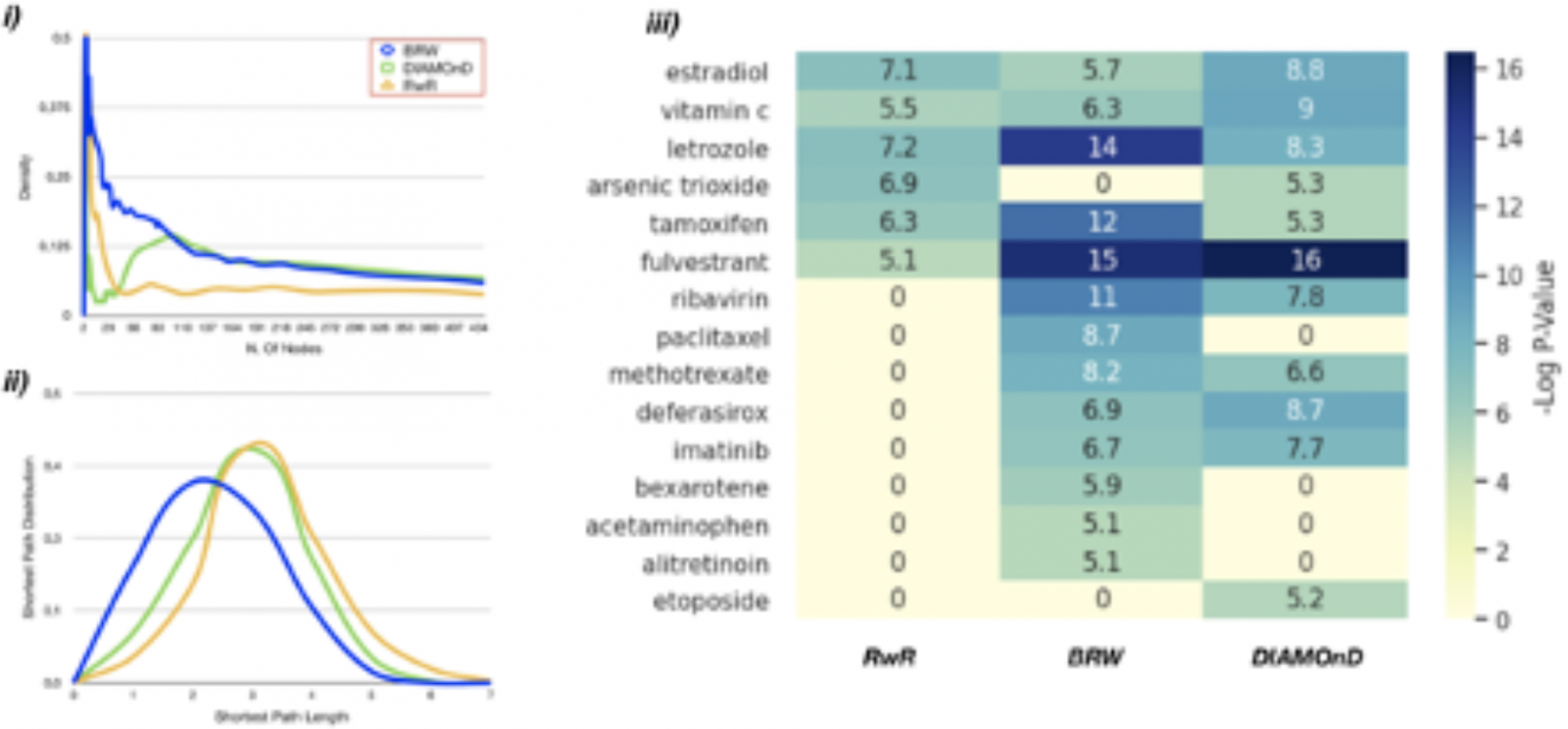
Figure 1: Disease module topology and drug enrichment validation.
Written by: Michele Gentili and Leonardo Martini
Revised by: Luca Pappalardo
References:
[1] Stephen Y Chan and Joseph Loscalzo. The emerging paradigm of net- work medicine in the study of human disease. Circulation research, 111(3):359–374, 2012.
[2] Mika Gustafsson, Colm E Nestor, Huan Zhang, Albert-L ́aszl ́o Barab ́asi, Sergio Baranzini, S ̈oren Brunak, Kian Fan Chung, Howard J Federoff, Anne-Claude Gavin, Richard R Meehan, et al. Modules, networks and systems medicine for understanding disease and aiding diagnosis. Genome medicine, 6(10):82, 2014.
[3] Albert-L ́aszl ́o Barab ́asi, Natali Gulbahce, and Joseph Loscalzo. Net- work medicine: a network-based approach to human disease. Nature reviews genetics, 12(1):56, 2011.
[4] Gentili, M., Martini, L., Petti, M., Farina, L., & Becchetti, L. (2019, July). Biological Random Walks: Integrating heterogeneous data in disease gene prioritization. In 2019 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB) (pp. 1-8). IEEE.

